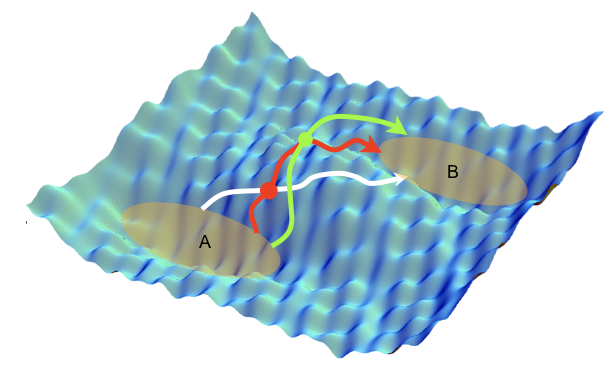
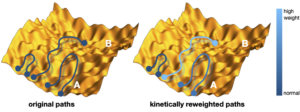
Molecular dynamics simulations are often combined with experimental data with the aim to improve structural molecular models. However, it is still unclear how to include experimental knowledge about kinetic, e.g. interconversion rates between different thermodynamically stable states. Recently we introduced a novel method of imposing known rate constants as constraints in such simulations, based on a combination of the maximum entropy and maximum caliber principles. The method corrects an initial dynamical path ensemble by reweighting it in order to match the calculated and experimental interconversion rates of a molecular transition of interest, yielding improved structure, kinetics and thermodynamics, as well mechanistic insights that may not be readily evident directly from the experiments. We anticipate that this method will extend the applicability of molecular simulations to kinetic studies in structural biology, and that it will assist the development of force fields to reproduce kinetic and thermodynamic observables. Furthermore, this approach is generally applicable to a wide range of systems in biology, chemistry, physics, and material science.
However, many open fundamental questions remain: how to deal with numerical instabilities that can appear in the method. How can machine learning techniques be used to avoid this? What is the role of the collective variable (CV) that is being used to parametrize the reaction progress. Can this CV be optimized using a new variational principle? Is this consistent with existing principles about optimized CVs?
In this project the student will apply this method using data generated with simple (toy) models, and existing molecular dynamics data on protein folding and conformational changes, together with existing experimental measurements. The project requires some programming skills, knowledge of python. Affinity with theory and mathematical modeling is recommended.
[1] A method of incorporating rate constants as kinetic constraints in molecular dynamics simulations. Z. F. Brotzakis, M. Vendruscolo, P. Bolhuis arXiv: 2006.00868 (2020)