Potential energy functions and their derivatives play an essential ingredient of molecule simulations. First and second derivatives of angle-dependent potentials are very tedious to derive (using application of chain-rules for derivatives), but very useful in molecular simulations. The angle is a complicated function of the atom positions. Computing normal modes requires the Hessian matrix, a matrix of second derivatives with respect to position. The Hessian is also of great use in efficient minimization methodology. Common planar molecules that contain a double bond or sp2 hybridization form planar groups with trigonal centers. For example: the carbon centers in benzene and carbon and nitrogen centers in formamide. The mode of motion is different from bond stretching, bending, and internal rotation.
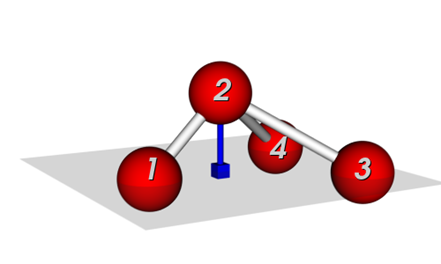
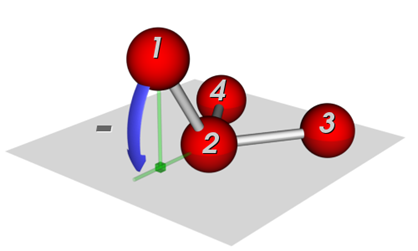
Two common definitions for out-of-plane potentials in use are (see Figure 1):
(i) the distance of the central atom from the plane defined by the other three atoms (pyramid height), and
(ii) the average angle between any bond that extends from the central atom and the plane defined by the other two bonds.
The out-of-plane potential can also be used for non-planar structures, for example in chiral-centers to avoid inversion.
No analytical expressions for the second derivatives with respect to position and/or strain have been published for out-of-plane potentials.
Figure 1: Potentials to keep connected atoms in a plane:, (a) Wilson-angle, (b) out-of-plane potential.
Aim
Derivation of analytical second derivatives with respect to position and strain for the out-of-plane and Wilson potential.
Reference
Design, Parameterization, and Implementation of Atomic Force Fields for Adsorption in Nanoporous Materials
D. Dubbeldam, K.S. Walton, T.J.H. Vlugt, and S. Calero
Adv. Theory Simulat., 2(11), 1900135 (2019).